Площадь треугольника через площадь описанной окружности

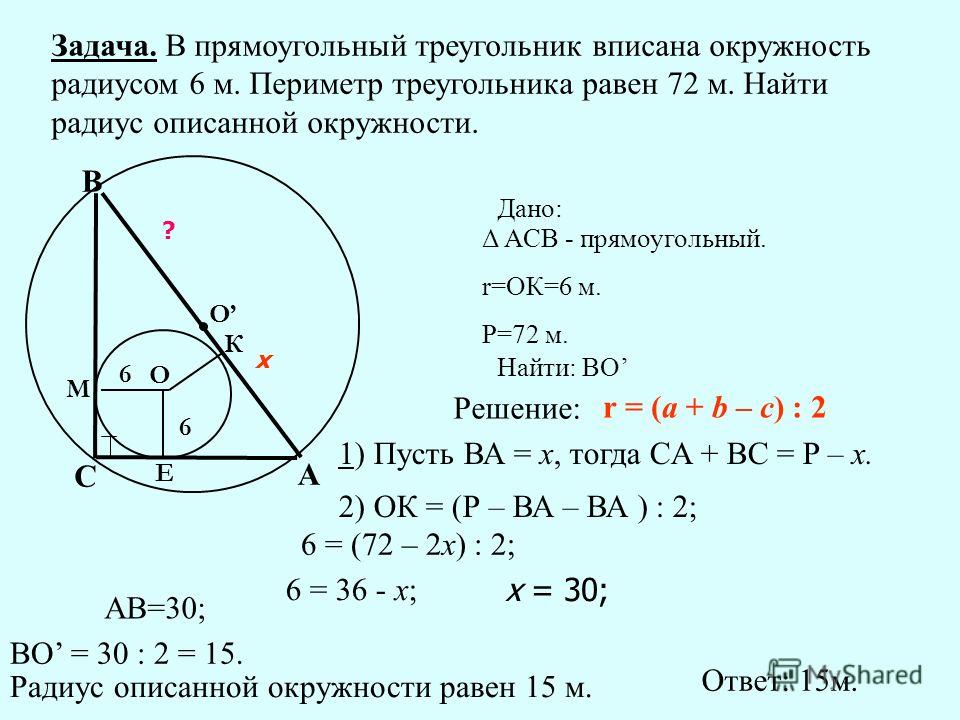
Из нее же можно найти и радиус описанной окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности. Около любого треугольника можно описать окружность. В этом случае окружность называется описанной вокруг треугольника. Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам.

A, B, C, и v находятся на одном и том же расстоянии r от общего центра u окружности. На рисунке показаны равные углы у треугольника, вписанного в окружность. Сторона, противоположная углу α, дважды касается окружности: один раз на каждом конце; в каждом случае под одинаковым углом α (см. рис.) (аналогично для двух других углов). 3 из 4 окружностей, описанных относительно серединных треугольников (образованных средними линиями треугольника), пересекаются в одной точке внутри треугольника.

Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны. Такие окружности называют полувписанными или окружностями Веррьера. Она служит центром гомотетии, которая переводит описанную окружность во вписанную. Точки касания окружностей Веррьера со сторонами лежат на прямой, которая проходит через центр вписанной окружности.

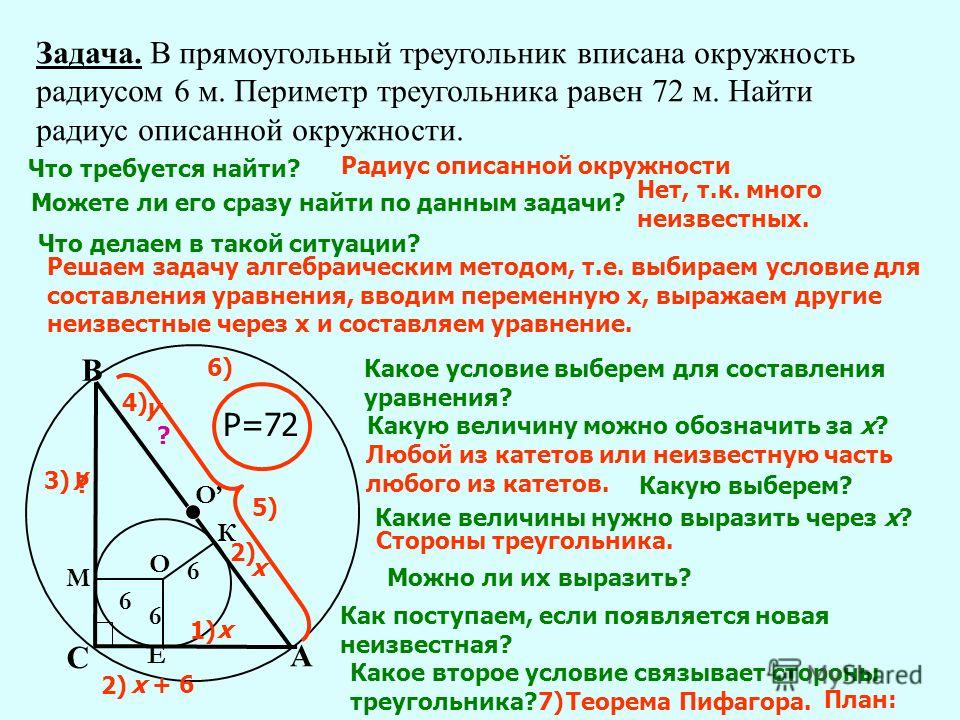
Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 180° (π{\displaystyle \pi } радиан). Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Если окружность описана вокруг прямоугольного треугольника, то ее центр будет лежать на середине гипотенузы. Довольно часто по условиям можно встретить данную площадь описанной окружности, которую необходимо использовать для нахождения площади вписанного треугольника.

Площадь треугольника через площадь описанной окружности

Зная все три стороны заданного треугольника можно применить для нахождения площади формулу Герона. То есть, зная длины всех сторон треугольника, мы можем найти площадь треугольника через радиус описанной окружности. Попробуем найти радиус по другой формуле, которую мы вывели из способа нахождения площади треугольника по трем сторонам. Зная несколько несложных формул, мы смогли найти площадь вписанного треугольника.

Внутри треугольника ABC взята произвольная точка O и через нее проведены три прямые, параллельные сторонам треугольника. Эти прямые делят треугольник ABC на шесть частей, три из которых являются треугольниками. Как найти радиус описанного круга. Как найти радиус описанной окружностиОкружность считается описанной вокруг многоугольника в том случае, если она касается всех его вершин.

Радиус описанной окружности полностью зависит от того многоугольника, вокруг которого она описана. С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку.

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Для определения гипотенузы рассматриваемого треугольника применяется теорема Пифагора. Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать в окружность можно только равнобокую трапецию.

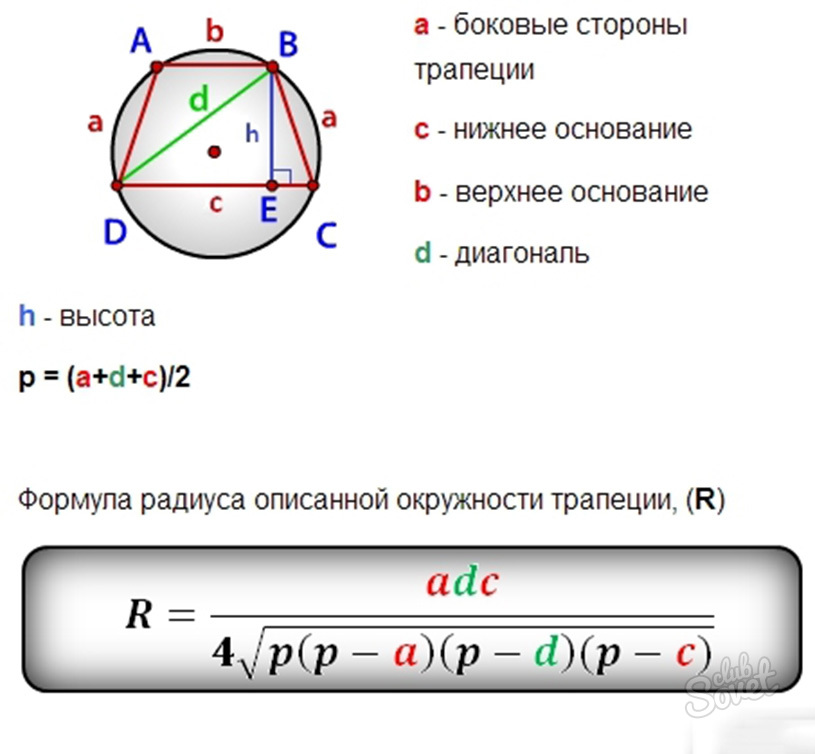
Радиус описанной около трапеции окружности можно найти по следствию из теоремы синусов. Кстати, использовать углы COD и CAD можно и для нахождения площади трапеции. Рассмотрим произвольный треугольник ABC и описанную вокруг него окружность, радиус которой обозначим через R (рис. 303). Пусть А — острый угол треугольника.

Координаты центра описанной окружности — Геометрия

Радиус описанной окружности равен отношению произведения трех сторон треугольника к его учетверенной площади. 1. Высота прямоугольного треугольника, проведенная из вершины прямого угла, делнт гипотенузу в отношении Найти отношение каждого из катетов к гипотенузе.

3. Две окружности касаются внешним образом. Их общие касательные наклонены к линии центров под углом 30°. Длина отрезка касательной между точками касания равна 108 см. Найти радиусы окружностей. 9. Известны стороны треугольника а, b, с. Чему равны отрезки, на которые они разбиваются точками касания вписанной окружности со сторонами треугольника? Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность.

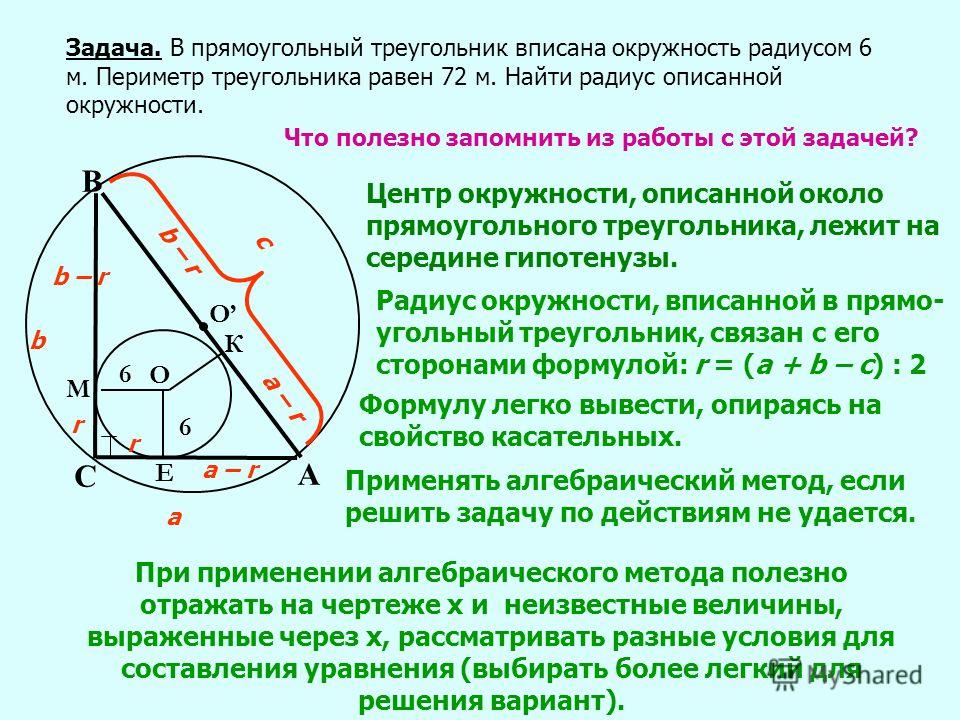
Свойства описанной около треугольника окружности. Теорема синусов

В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам.

Пусть дан треугольник со сторонами a = 5 см, b = 6 см, c = 4 см. Вокруг него описана окружность с R = 3 см. найдите площадь. Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.