Площади ромба через сторону и угол

Площадь квадрата равна квадрату длины его стороны: где a — сторона квадрата. 45°. Найдите AB, если площадь трапеции ABCD равна 10.С-15. Площадь треугольника. Площадь параллелограмма равна произведению параллелограмма на высоту проведённую к этой стороне. 27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры).

Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Площади ромба через сторону и угол

Ромб с прямыми углами называется квадратом и считается частным случаем ромба. Найти площадь ромба можно различными способами, используя все его элементы – стороны, диагонали, высоту. Классической формулой площади ромба считается расчет значения через высоту. Пример расчета площади ромба по этой формуле очень прост. Необходимо только подставить данные и высчитать площадь.

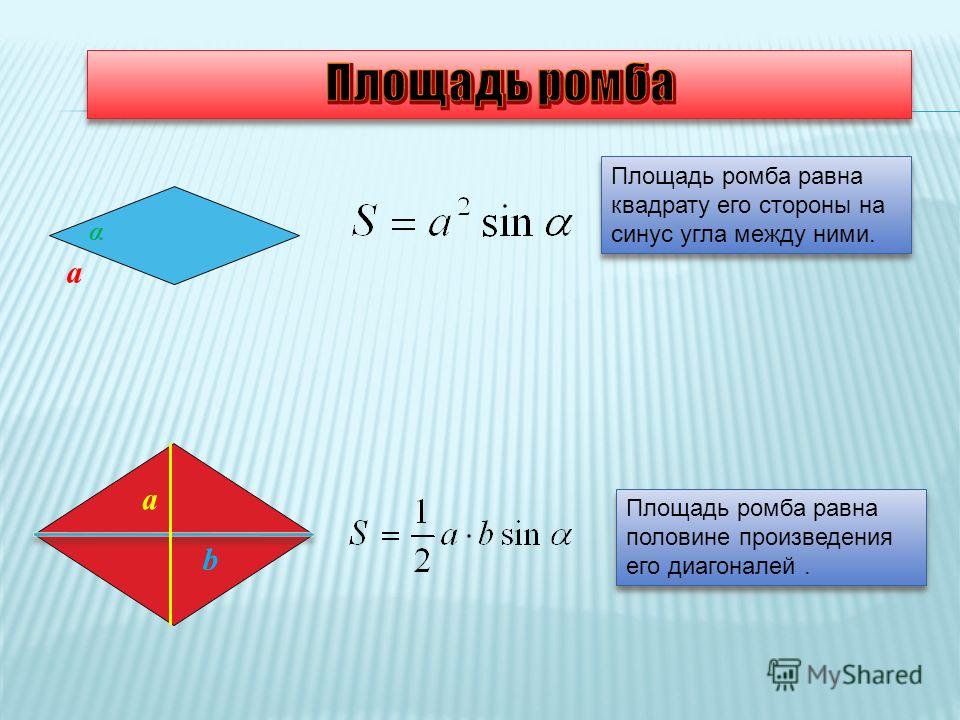
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам. Рассмотрим пример расчета площади ромба через диагонали. 1=5 см и d2=4. Найдем площадь. Пример расчета площади ромба через стороны также весьма прост. Требуется только просчитать радиус вписанной окружности.

Совет 1: Как найти площадь ромба

Для начала найдем сторону ромба. Используем для этого теорему Пифагора. Ромб впервые вводят древнегреческие математики Герон и Паппа Александрийский. А ромб с прямыми углами можно смело назвать квадратом. Подробно было написано про диагонали ромба, что не зря, потому что они используются в формуле для нахождения площади.

Формула вычисление площади ромба, содержащая синус угла, не единственная. Все значения известны и понятны, кроме появившегося r — это максимальный радиус окружности, который может поместиться в фигуре. Эти дополнительные свойства четырехугольника значительно упрощают формулы нахождение его площади. Если известны длины обеих диагоналей ромба (E и F), то для нахождения площади фигуры (S) рассчитайте значение половины произведения этих двух величин: S=½*E*F.

Если кроме радиуса вписанной окружности (r) известна только величина острого угла (α) ромба, то в этом случае тоже можно задействовать тригонометрическую функцию. Подставьте соответствующие значения в формулу из первого шага и выясните, что площадь в этом случае можно найти, удваивая возведенный в квадрат радиус: S=2*R².

SΔ — площадь треугольника с вершинами в центре круга и в концах радиусов, ограничивающих соответствующий сектор. Площадь полной поверхности прямоугольного параллелепипеда. Площадь боковой поверхности конуса. Диагонали ромба — это линии, соединяющие противоположные углы в центре фигуры. Диагонали ромба перпендикулярны и после пересечения образуют четыре правильных треугольника. В нашем случае это составит 6 см x 8 см = 48 см2. Не забывайте указывать квадратные единицы, так как вы работаете с квадратной площадью.

Вы можете также подумать об этом как об умножении высоты ромба на длину стороны. Зная основание и высоту ромба, вам остается только умножить одно на другое. У ромба имеется четыре равные стороны, так что не важно, какую именно вы выберете. O и является центром вписанной в дельтоид окружности. Каждое из отношений стороны к синусу противолежащего угла равно 2R, где R — радиус окружности, описанной около треугольника.

Определение и формула площади треугольника через синус

В равнобедренном треугольнике (длины боковых сторонравны) высота, проведенная к основанию, является медианой и биссектрисой. Внешний угол треугольника (∠4) равен сумме двух внутренних, не смежных с ним, т. е. ∠4=∠1+∠2. Средняя линия треугольника параллельна основанию и равна его половине: MN=AC/2. Центр тяжести треугольника — точка пересечения медиан, которая делит каждую медиану в отношении 2:1, считая от вершины.

Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис углов треугольника. Боковая и полная поверхности, а также объем можно находить по тем же формулам, что и в случае прямой призмы. 3) стороны одного треугольника равны соответствующим сторонам другого треугольника.

Пример 1. Площадь равнобедренного остроугольного треугольника равна 12, а длина высоты, опущенной на боковую сторону, . Найдите угол при основании. Он состоит в том, что площадь треугольника выражается через разные элементы. Пример 2. Один из катетов прямоугольного треугольника в два раза больше другого.

используя основание и высоту

Стороны AO и OC являются радиусами окружности. Треугольником называется фигура, состоящая из трех вершин и трех сторон. Существует много формул для вычисления площади треугольника. Уровни фигуры имеют равные площади. Где a и b — смежные стороны прямоугольника. Самая простая решается как сложение площадь 2 треугольников, которые получились в результате деления диагоналей.

Третью формулу можно использовать когда знаешь угол между сторон. Зная его можно найти площадь ромба, она будет равна квадрату сторон на синус угла. При чем нет разницы какой угол. так как синус угла имеет единое значение. Важно помнить что измерение площади происходит в квадратах, а периметра в единицах.

Так же могут встретиться задачи на поиск радиуса по вписанной в ромб окружности. В помощью первой формулы радиус находится как произведение диагоналей поделенное на число полученное от сложения всех сторон. В третьей формуле радиус выходит из высоты меньшего из треугольников, получившегося в результате пересечения. Здравствуйте! В этой статье представлена группа заданий решение которых связанно с площадью параллелограмма.

Если у параллелограмма в котором биссектриса это диагональ, то он называется ромбом. Ромб — это четырехугольный параллелограмм с четырьмя равными сторонами, площадь которого можно вычислить по четырем разным формулам. Известно, что AB > BC > KC, а периметр и площадь треугольника BKC равны соответственно 14 и 7. Найдите DC.С-14.